hybridlane¶

Submodules¶

Attributes¶

`SQR`	number-Selective Qubit Rotation (SQR) gate`
`SNAP`	Selective Number-dependent Arbitrary Phase (SNAP) gate
`Red`	Red sideband gate
`Blue`	Blue sideband gate
`P`	Momentum operator \(\hat{p}\)
`X`	Position operator \(\hat{x}\)
`N`	Number operator \(\hat{n}\)

Classes¶

`Rotation`	Phase space rotation gate \(R(\theta)\)
`Displacement`	Phase space displacement gate \(D(\alpha)\)
`Squeezing`	Phase space squeezing gate \(S(\zeta)\)
`Kerr`	Kerr gate \(K(\kappa)\)
`TwoModeSum`	Two-mode summing gate \(SUM(\lambda)\)
`TwoModeSqueezing`	Phase space two-mode squeezing \(TMS(r, \varphi)\)
`Beamsplitter`	Beamsplitter gate \(BS(\theta, \varphi)\)
`QuadOperator`	The generalized quadrature observable \(\hat{x}_\phi = \hat{x} \cos\phi + \hat{p} \sin\phi\)
`CubicPhase`	Cubic phase shift gate \(C(r)\)
`ModeSwap`	Continuous-variable SWAP between two qumodes
`Fourier`	Continuous-variable Fourier gate \(F\)
`Hybrid`	Mixin for hybrid CV-DV gates
`SelectiveQubitRotation`	number-Selective Qubit Rotation (SQR) gate \(SQR(\theta, \varphi, n)\)
`SelectiveNumberArbitraryPhase`	Selective Number-dependent Arbitrary Phase (SNAP) gate \(SNAP(\varphi, n)\)
`JaynesCummings`	Jaynes-cummings gate \(JC(\theta, \varphi)\), also known as Red-Sideband
`AntiJaynesCummings`	Anti-Jaynes-cummings gate \(AJC(\theta, \varphi)\), also known as Blue-Sideband
`Rabi`	Rabi interaction \(RB(\theta)\)
`ConditionalDisplacement`	Symmetric conditional displacement gate \(CD(\alpha)\)
`ConditionalSqueezing`	Qubit-conditioned squeezing gate \(CS(\zeta)\)
`ConditionalRotation`	Qubit-conditioned phase-space rotation \(CR(\theta)\)
`ConditionalParity`	Qubit-conditioned number parity gate \(CP\)
`ConditionalBeamsplitter`	Qubit-conditioned beamsplitter \(CBS(\theta, \varphi)\)
`ConditionalTwoModeSqueezing`	Qubit-conditioned two-mode squeezing \(CTMS(\xi)\)
`ConditionalTwoModeSum`	Qubit-conditioned two-mode sum gate \(CSUM(\lambda)\)
`QuadP`	The momentum quadrature observable \(\hat{p}\).
`QuadX`	The position quadrature observable \(\hat{x}\).
`NumberOperator`	The photon number observable \(\langle \hat{n}\rangle\).
`FockStateProjector`	The number state observable \(\ket{n}\bra{n}\).
`FockLadder`	Prepares a definite Fock state from the vacuum

Functions¶

`draw_mpl`(qnode[, wire_order, show_all_wires, ...])	Draws a circuit using matplotlib
`to_openqasm`(qnode[, rotations, precision, strict, ...])	Converts a circuit to an OpenQASM 3.0 program
`expval`(op)	Expectation value of the supplied observable
`var`(op)	Variance of the supplied observable

Package Contents¶

hybridlane.draw_mpl(qnode, wire_order=None, show_all_wires=False, show_wire_types=True, decimals=None, style=None, *, max_length=None, fig=None, level='gradient', **kwargs)[source]¶

Draws a circuit using matplotlib

Parameters:

qnode (QNode | Callable) – The circuit to be drawn
wire_order (Sequence | None) – The display order (top to bottom) of wires in the circuit
show_all_wires (bool) – Whether to show all wires or just those that are used
show_wire_types (bool) – Whether to draw qubit/qumode icons next to each wire label
decimals (int | None) – The number of decimals to print circuit parameters with. If not provided, parameters won’t be shown.
style (str | None) – The drawing style to use. See qml.draw_mpl.
max_length (int | None)
level (Literal['top', 'user', 'device', 'gradient'] | int | slice | None)

Keyword Arguments:

wire_icon_colors (dict) – A dictionary mapping wires to optional matplotlib-compatible colors. All wires that aren’t provided will use default qubit or qumode colors.

For other arguments, see qml.draw_mpl.

Returns:

A function that when called, produces the same output as qml.draw_mpl

Parameters:

qnode (QNode | Callable)
wire_order (Sequence | None)
show_all_wires (bool)
show_wire_types (bool)
decimals (int | None)
style (str | None)
max_length (int | None)
level (Literal['top', 'user', 'device', 'gradient'] | int | slice | None)

Examples

By default, Hybridlane draws quantum circuits with wire icons and default colors.

@qml.qnode(dev)
def circuit(n):
    for j in range(n):
        qml.X(0)
        hqml.JaynesCummings(np.pi / (2 * np.sqrt(j + 1)), np.pi / 2, [0, 1])

    return hqml.expval(hqml.NumberOperator(1))

n = 5
hqml.draw_mpl(circuit, style="sketch")(n)

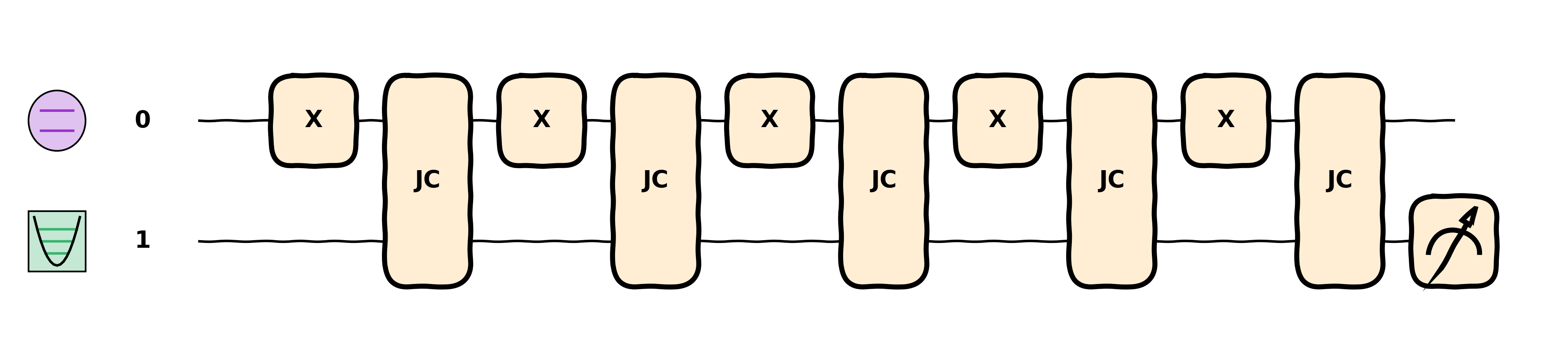
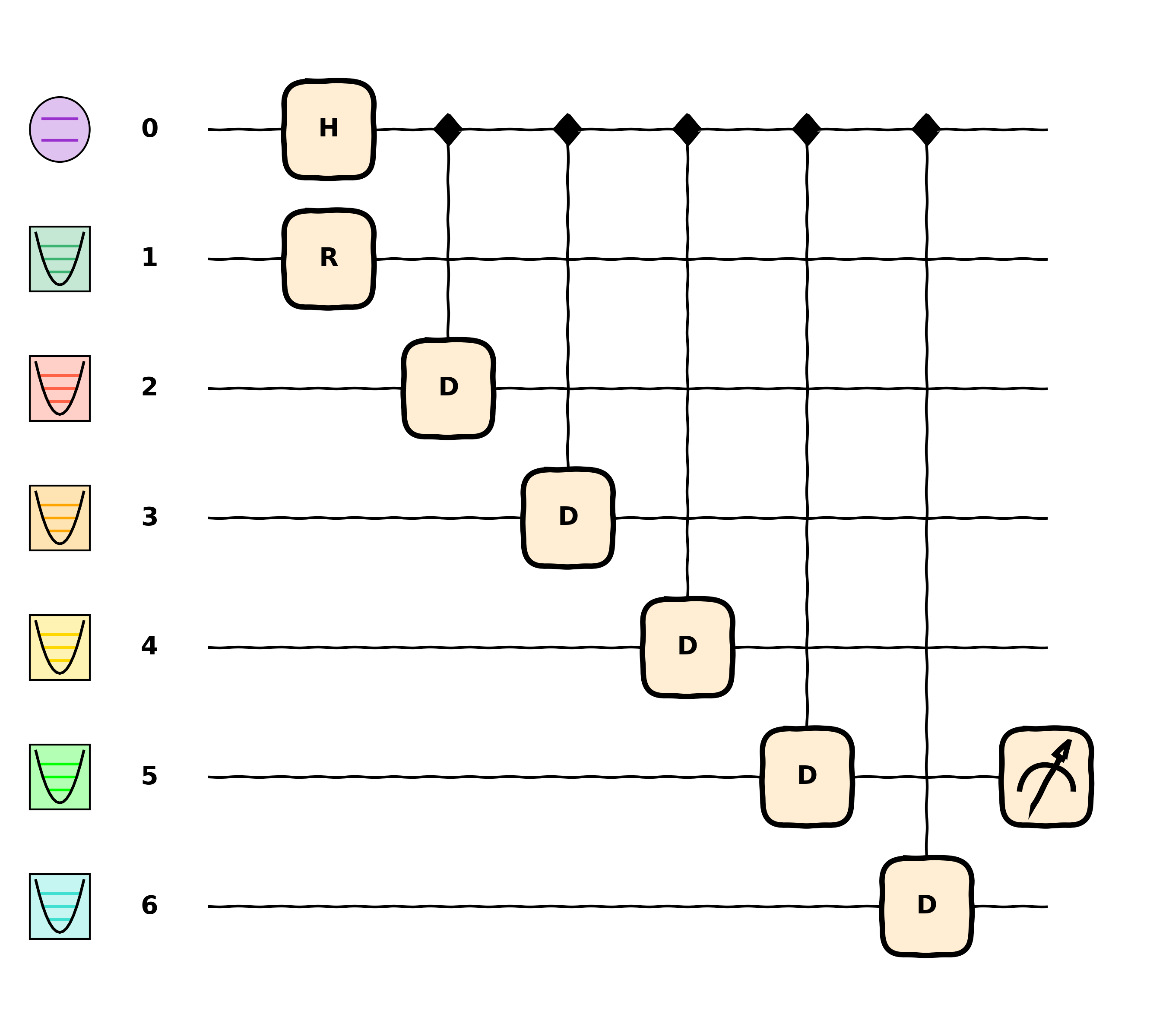
Furthermore, icon colors can be adjusted from their defaults (say to color different motional modes of an ion trap). Note that Hybridlane also has a special notation for “qubit-conditioned” gates.

@qml.qnode(dev)
def circuit(n):
    qml.H(0)
    hqml.Rotation(0.5, 1)

    for i in range(n):
        hqml.ConditionalDisplacement(0.5, 0, [0, 2 + i])

    return hqml.expval(hqml.NumberOperator(n))

icon_colors = {
    2: "tomato",
    3: "orange",
    4: "gold",
    5: "lime",
    6: "turquoise",
}

hqml.draw_mpl(circuit, wire_icon_colors=icon_colors, style="sketch")(5)

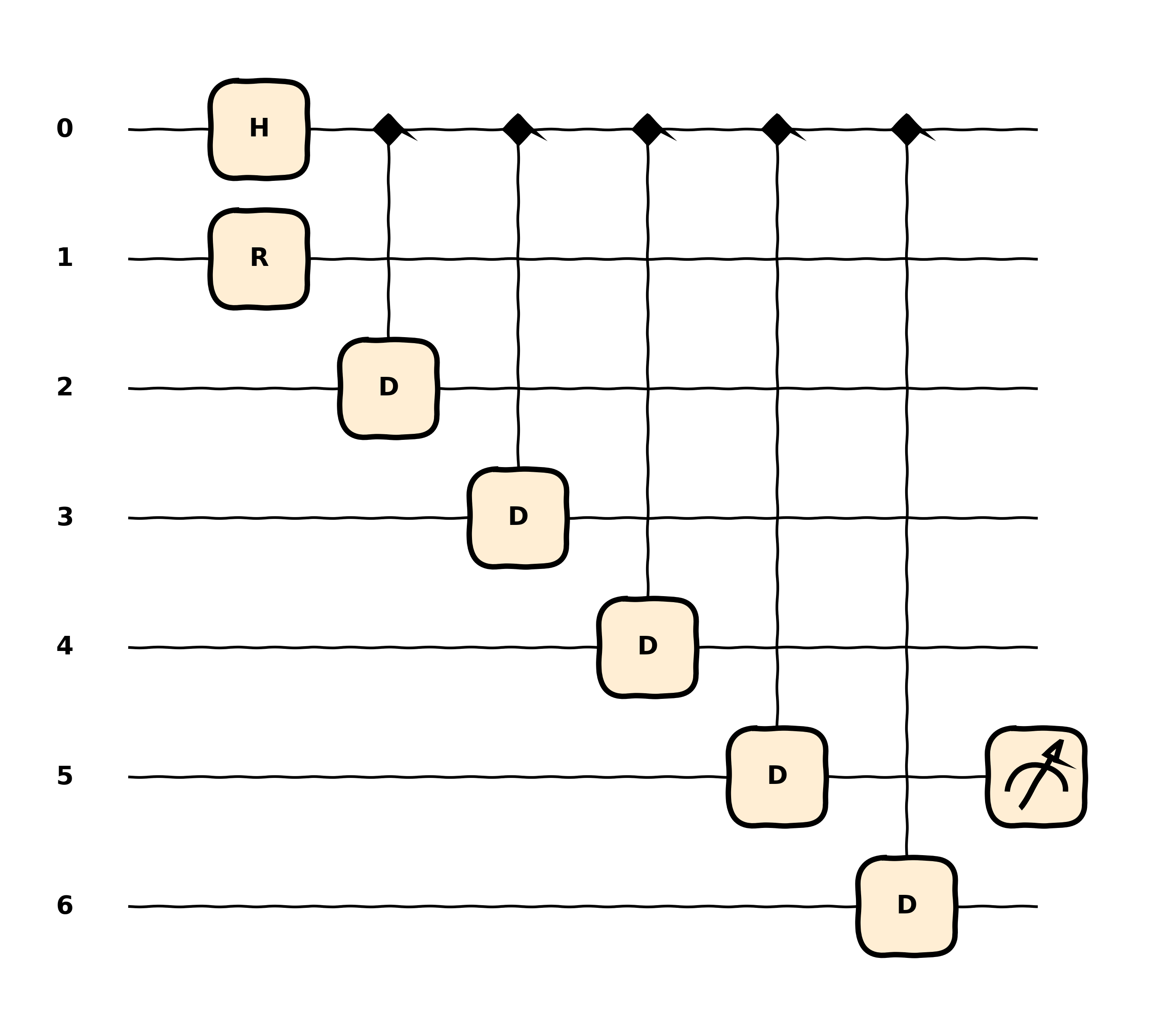
Finally, if you don’t like pretty icons, you can disable them.

@qml.qnode(dev)
def circuit(n):
    qml.H(0)
    hqml.Rotation(0.5, 1)

    for i in range(n):
        hqml.ConditionalDisplacement(0.5, 0, [0, 2 + i])

    return hqml.expval(hqml.NumberOperator(n))

hqml.draw_mpl(circuit, show_wire_types=False, style="sketch")(5)

hybridlane.to_openqasm(qnode, rotations=True, precision=None, strict=False, float_bits=32, int_bits=32, indent=4, level='user')[source]¶

Converts a circuit to an OpenQASM 3.0 program

By default, the output will be a superset of the OpenQASM standard with extra features and language extensions that capture hybrid CV-DV programs. These modifications are detailed in the documentation. If you would like the output to be strictly compliant with OpenQASM 3.0, you can pass the strict=True flag, which will

Replace measure_x and measure_n keywords with equivalent defcal statements and function calls.
Remove all qumode keywords, replacing them with qubit. This has the effect of erasing the type information of the program.

Note

Qubit measurements are assumed to be performed in the computational basis, while qumode measurements are determined from the BasisSchema of each measurement. If sampling an observable, this function can provide the gates necessary to diagonalize each observable by setting rotations=True. Only wires that are actually measured will have measurement statements. Finally, non-overlapping measurements will be grouped together as much as possible and measured on the same call to state_prep(); however, the resulting program may have multiple executions of the tape as needed to accomodate all the measurements.

Parameters:

qnode – The QNode to be converted to OpenQASM
rotations (bool) – Include diagonalizing gates for an observable prior to measurement. This applies both to qubit observables and qumode observables.
precision (int | None) – An optional number of decimal places to use when recording the angle parameters of each gate
strict (bool) – Forces the output to be strictly compliant with the OpenQASM 3.0 parser.
float_bits (int) – The number of bits used to contain the result of a homodyne measurement.
int_bits (int) – The number of bits used to contain the result of a Fock state readout.
indent (int) – Number of spaces to indent the program by
level (str | None)

Returns:

A string containing the program in OpenQASM 3.0

Return type:

Callable[[Any], str]

hybridlane.expval(op)[source]¶

Expectation value of the supplied observable

Parameters:: op (Operator | pennylane.measurements.mid_measure.MeasurementValue)
Return type:: ExpectationMP

hybridlane.var(op)[source]¶

Variance of the supplied observable

Parameters:: op (Operator | pennylane.measurements.mid_measure.MeasurementValue)
Return type:: VarianceMP

hybridlane.SQR¶: number-Selective Qubit Rotation (SQR) gate`

\[SQR(\theta, \varphi) = R_{\varphi}(\theta) \otimes \ket{n}\bra{n}\]

See also

This is an alias for SelectiveQubitRotation

hybridlane.SNAP¶: Selective Number-dependent Arbitrary Phase (SNAP) gate

\[SNAP(\varphi, n) = e^{-i \varphi \sigma_z \ket{n}\bra{n}}\]

See also

This is an alias for SelectiveNumberArbitraryPhase

hybridlane.Red¶: Red sideband gate

\[JC(\theta, \varphi) = \exp[-i\theta(e^{i\varphi}\sigma_- \ad + e^{-i\varphi}\sigma_+ a)]\]

See also

This is an alias of JaynesCummings

hybridlane.Blue¶: Blue sideband gate

\[AJC(\theta, \varphi) = \exp[-i\theta(e^{i\varphi}\sigma_+ \ad + e^{-i\varphi}\sigma_- a)]\]

See also

This is an alias of AntiJaynesCummings

hybridlane.P¶: Momentum operator \(\hat{p}\)

See also

This is an alias for QuadP

hybridlane.X¶: Position operator \(\hat{x}\)

See also

This is an alias for QuadX

hybridlane.N¶: Number operator \(\hat{n}\)

See also

This is an alias for NumberOperator